Project
2022/03/27
News
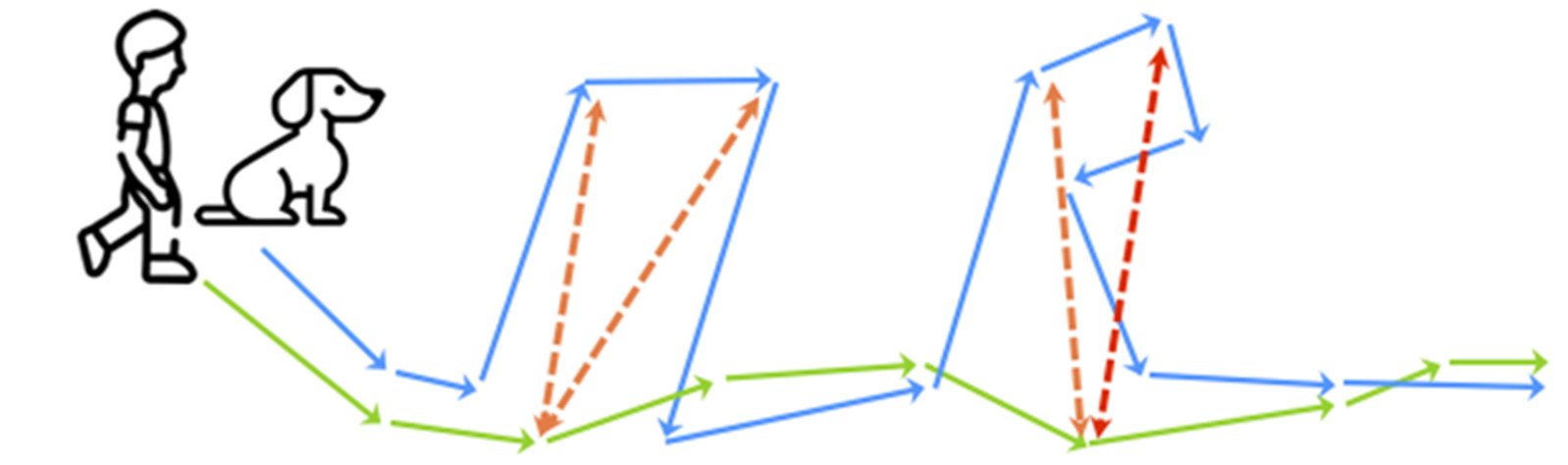
Frechet Kernel for Trajectory Data Analysis (SIGSPATIAL2021)
We proposed a trajectory kernel with smoothed Fréchet distance and Hausdorff distance and its fast computation algorithms whose original distances are widely used in the field of spatial data analysis to measure the similarity of trajectory data. We applied our proposed distances to real trajectory data analysis using data obtained from automobiles, bicycles, pedestrians, wild animals, and physical This research has been accepted to the ACM SIGSPATIAL 2021.
[Proceedings: https://dl.acm.org/doi/10.1145/3474717.3483949]
[code: https://github.com/koh-t/frk]
@inproceedings{10.1145/3474717.3483949,
author = {Takeuchi, Koh and Imaizumi, Masaaki and Kanda, Shunsuke and Tabei, Yasuo and Fujii, Keisuke and Yoda, Ken and Ishihata, Masakazu and Maekawa, Takuya},
title = {Fr\'{e}chet Kernel for Trajectory Data Analysis},
year = {2021},
isbn = {9781450386647},
url = {https://doi.org/10.1145/3474717.3483949},
doi = {10.1145/3474717.3483949},
booktitle = {Proceedings of the 29th International Conference on Advances in Geographic Information Systems},
series = {SIGSPATIAL ’21}
}
Summary:
Trajectory analysis has been a central problem in applications of location tracking systems. Recently, the (discrete) Fr\'{e}chet distance becomes a popular approach for measuring the similarity of two trajectories because of its high feature extraction capability. Despite its importance, the Fr\'{e}chet distance has several limitations: (i) sensitive to noise as a trade-off for its high feature extraction capability; and (ii) it cannot be incorporated into machine learning frameworks due to its non-smooth functions. To address these problems, we propose the Fr\'{e}chet kernel (FRK), which is associated with a smoothed Fr\'{e}chet distance using a combination of two approximation techniques. FRK can adaptively acquire appropriate extraction capability from trajectories while retaining robustness to noise. Theoretically, we find that FRK has a positive definite property, hence FRK can be incorporated into the kernel method. We also provide an efficient algorithm to calculate FRK. Experimentally, FRK outperforms other methods, including other kernel methods and neural networks, in various noisy real-data classification tasks.